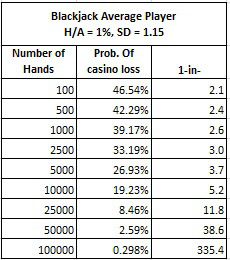
After 100 hands, 46.5% of these average players will be beating the house. After 10,000 hands, the percentage still beating the house has dropped to 19.2%. At a game pace of 100 hands per hour, nearly one-in-five average skill players will be beating the house after 100 hours of play. The striking result, however, is the bottom line in this table. After 100,000 hands, about 1000 hours of play, one player in 335 will still be beating the house.

There is nothing the casino can do about these lucky players. They must exist, purely by chance. No amount of "getting even" can change statistical inevitability. In a large casino, there are going to be quite a few players whose luck appears to persist beyond reason. If one of these players happens to be a high-roller, things can get ugly. Often, valuable resources are expended investigating the player. Sometimes, the casino just kicks the player out for no good reason, saying something like "we can't beat this guy." Often, there is no logical argument that is effective with management when they face such a player. They view the player's future results as likely to be similar to the player's past results - in other words, they expect this player to continue winning.

Conversely, I cannot tell you the number of times someone has told me how their relative, friend or colleague is a "professional" who always beats the house. I've stopped doubting these people; they are right, of course. Their associate has been beating the house over the course of hundreds of hours. The annoying consequence, however, is when these players write books, post on message boards or brag in public about their knowledge and skills. They often have flimsy arguments about how they achieved their success and will defend their position with mockery and double-talk. There is no argument that can convince such a player that he is just one of the lucky guys who must exist by virtue of the probabilistic model for the game.

The following table shows the number of hands it takes to achieve a certain confidence of beating a player. I have listed the results for both the average player we considered above, as well as for a perfect basic strategy player who is playing a standard double-deck game:

For example, consider the entry under 90%, corresponding to the generic player. This table shows that it requires 21720 hands before the casino has a 90% chance of beating the average player. Put another way, 10% of all generic players will still be beating the house after 21720 hands. Likewise, after 126293 hands, the casino will have a 99.9% chance of beating the average player. In other words, one player in 1000 will still be beating the house after 126293 hands, purely by chance. If that player happens to be a high-roller, he will surely pose a significant managerial and game protection problem for the casino.

Now consider the perfect basic strategy player listed in the top row. In this case, the number of hands required to achieve various levels of confidence increase dramatically. It now requires 145298 hands to have 90% confidence in beating such a player. It requires a stunning 478480 hands to have 99% confidence. Put another way, after 478480 hands, one perfect basic strategy player in 100 will still be beating the house! This is more than a lifetime of blackjack hands for most players. In simple terms, if a player is using perfect basic strategy, there can be no reasonable long-term expectation of beating the player.

Over the entire population of players a casino sees, there will be a significant number of long-term winners, even among average skill-level players. To see this statistical inevitability in another light, I conducted a simulation of 25 perfect basic strategy players. In this simulation, I assumed the game they played (6D, H17, DOA, DAS) had a house edge of 0.61%. Each player played 100,000 hands and I tracked and plotted their result along the way. The following picture shows the results of this simulation (click on the image to make it larger):

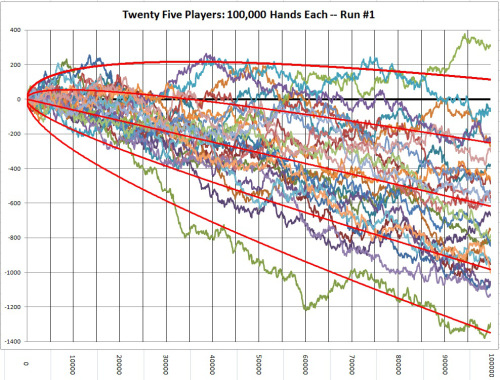
The straight red line in the middle indicates the "theoretical loss" of the players. This line represents the amount the casino expects to win from the player after the given number of hands. The curved red lines above and below this straight line indicate +2, +1, -1, and -2 standard deviations from theoretical, respectively. The current result for each of the 25 players, as a function of the number of hands played, is plotted from left to right in terms of "units" won or loss.

Note that there is one player out of these 25 who finished ahead after 100,000 hands (see the top green line). This player finished ahead by about 300 units. If his unit was $10, then his win would be $3,000 and no one would notice or care. But if his unit was $1000, then his win would be $300,000 and he would become a focus of investigation. How does this player view himself? Most likely he and his friends are convinced that he is a skilled player, even if he has no idea what that skill is.

On the other hand, the green player on the bottom is certainly very unlucky, being about two standard deviations below normal in his results. After 100,000 hands, this player has lost about 1300 units. With a wager of $10, this player has lost about $13,000. If this player is a high-roller with a $1000 unit, then he would have lost about 1.3M. How does this player view himself? He is a big-time loser at blackjack who is just sick of seeing other players do better than him, but can't figure out what he is doing wrong.

There was one other player who finished nearly even after 100,000 hands. There were three other players in this simulation that finished with a loss of at least 1000 units. It is an interesting exercise to invent story lines from both the casino perspective and the player perspective for each of these players.

Here are 25 more players (again, click on the image to make it larger):

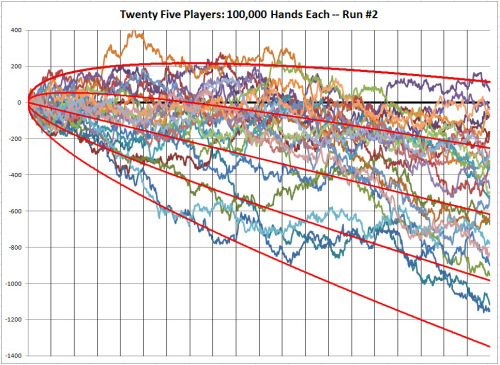
There is nothing the casino can do about the variety of results players have. There is nothing that players can do to choose their line. Some players will get lucky, other will be unlucky. The casino should not back off or exclude winners. Winning players should not delude themselves.

When I showed these simulations to a senior vice president of marketing for a major casino, she asked if it wasn't inevitable that each line eventually should converge to the straight line in the middle of the graph. She believed that in the long run, each player's results should be roughly equal to their theoretical loss. In other words, winners should lose and losers should win. No. Then she asked if losing and winning players would continue to lose/win at a similar rate. Again, No.  It's not just table games and surveillance who sometimes swing and miss.

Going forward, future results are independent of past results. Nothing a player has done in the past has any relevance to that player's results in the future. This holds true for average players and basic strategy players. At the end of the 100,000 hands, every player is subjected to the same forward-looking probabilities as every other player. The cards have no memory. The gambling fallacy that the past is relevant to the present is part of the flawed evolutionary wiring of the human mind.